Category: Math

Posted on

Tackling the Wonderful SAT TEST

SAT is literally in 3 days! That is scary but excited at the same time. In Math essential, 95% of the class time is strongly devoted to SAT math section preparation and I been doing that for over 4 weeks now.

Most of the time, we worked on filling the individual math content, such as the system of equation, right triangle, circle theorem, and remainder theorem. I pretty confident with the materials, but my two biggest flaws are the limited time and strategy that I approach the questions.  

Jeff Boucher, our math facilitator, had guided me through the differences approach to solving a problem. Those approaches include the plugin, read the desire findings, and work back from the answer choices.

As I spend some time working on different types of problems, I started to see some patterns and methods that work for me.

The only way to beat the time constraint and the test is to practice. So, I hope everything going to turn out well.

See you SAT!!

 

Posted on

Distance – Time graph word problem

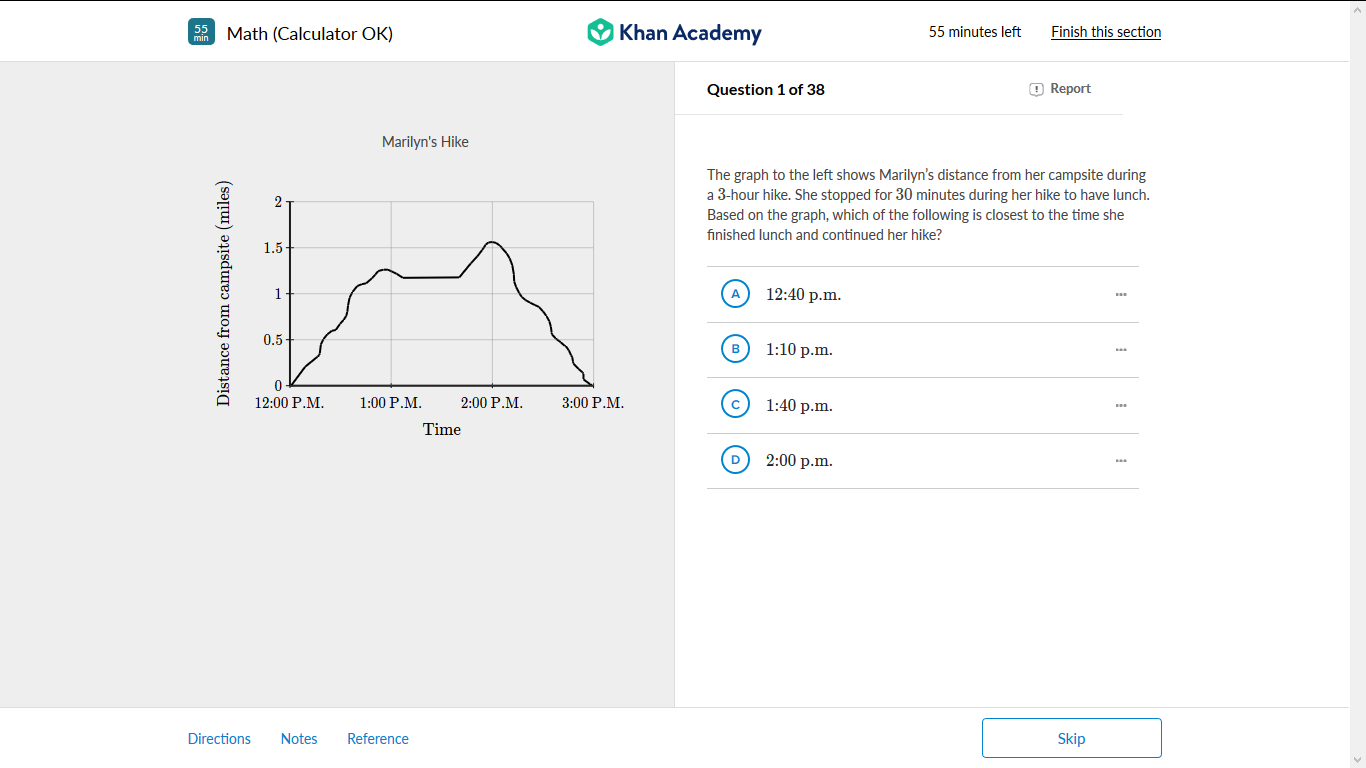
The distance, time graph show the position of Mrs. Kanha goes to different places from her home. Mrs. Kanha drove to a bookstore from her house to buy some books for her kids. After, her purchase on -the bookstore, she then drove to the gym to exercise so she remains fit and strong. Finally, she drove to her kids’ school to pick them up. The diagram below shows the distance, time graph of Mrs. Kanha.

Questions:

  1. How far is the bookstore away from the house?
  2. How far is the school to Mrs. Kanha home?
  3. Mrs. Kanha driving speed from her home to the bookstore was 8 km/h slower than her driving speed from the school to her home. Form an equation in x and solve it.
  4. Hence, express the time that Mrs. Kanha spent driving as a percentage of her whole journey.

Solution

  1. The distance from the house to the bookstore is 20 km.
  2. The distance from the school to Mrs. Kanha house is 25 km.
  3. First, we need to find the driving speed from her home to the bookstore.

Which give us that speed= 20 km / x minutes

Now, the unit is in km/minutes, we need to time 60 to the numerator to convert to km/hr, so that we can plus it with the 8 km/hr that they give us.

                = (20 * 60) / x

                = 1200 / x

Second, we need to find to the driving speed from the school home.

                Then, speed = 25 / 210-(x+105)

                After we have that, we need to do the same thing to make this to km/hr.

                Speed = 25 * 60 / 210-(x+105)

                =  1500 / 210-x-105

Third step is to take these two values and the information that they provide and turn to an equation.

                The easiest way is to make a words based equation and for this example there are three way you can set up.

                Therefore, the equations are:

                          1. Home → bookstore + 8 km/hr = school → home

                          2. School → home – home → bookstore = 8 km/hr

                          3. School → home – 8 km/hr = home → bookstore

                For this example, let’s pick equation number one.

                               (1200 / x )+ 8 = 1500 / 105-x

                               (1200 / x) + ((8*x) / (1*x)) = 1500 / 105-x

                               (1200+8x) / x = 1500 / 105-x

                               1500x = (8x + 1200)(-x + 105)

                               1500x = -8x^2 + 840x – 1200x + 126000

                               8x^2 + 1860x – 126000 = 0

                               (8x^2 + 1860x – 126000) / 4

                               2x^2 + 465x – 31500 = 0

                Now, we need to solve of x, there are many way we can solve of x, we can factor, graph and solve it or you can use the quadratic formula to isolate x.

                             For this example, let use the quadratic formula because the                                   other option is very hard to deal with huge numbers.

                                  Coefficient are: a = 2 ; b = 465 ; c =-31500

                                  Quadratic formula: x =  -b +- sqrt(b^2 – 4ac) / 2a

                                  Plug it a,b and c:  x = -465 +- sqrt(465^2 -4(2)(-31500) / 2(2)

                                  Solve: x= -465 +- sqrt(216225- -252000) / 4

                                  x= -465 +- sqrt(468225) / 4

                                  x=54.817 or x=-287.317 (rejected)

                         So, x=54.817 because there is no negative time.

4. To figure out Mrs. Kanha total driving time, we need to find out her total time of her journey and minus it with her rest time.

                 Find her total time: x+(x+46)+(x+97)+(x+105)+210

                 Plug the value of x in: 677.27 minutes

                 Her total time = 677.27 minutes

                 Her total rest time: (((x+46)-x)/3)*2)+((x+97)-(x+46))

                 Equal= 81.66 minutes

Then, we take her total time – her total rest time to find her total driving time

                 677.27 – 81.66 = 595.61 minutes

                 Required percentage = 595.61/677.27 * 100 = 87.9%

So, the percentage that she is driving compared to the whole trip is 87.9%

Posted on

AP Statistic

We has jump another big step in Math. This year in Math essential, I’m taking a college course, AP Statistic, which is a very challenging and involve a very high critical thinking skill. Not like other math we are doing, AP stat is quite fun, it is more to thinking about all world data rather than calculating the math like algebra. Moreover, I personally think that AP stat course will be more applicable to me in everyday life and in my further work. AP Stat is a lot of looking a bunch of data from whatever you want to investigate and analyse the association of those data. For example, I can collect data of people from various level of education and their income, then I can uses these data to analyse the correlation and the association between these two variables. The two main textbooks that we used to learn the materials are The Practice of Statistics and the Barron AP statistic test book. However, as we learning the concept, we realize that it is not enough, therefore, we uses many more online resource such as Khan academy, Edx course video and many others worksheet out there. So far, we finished four chapter:

  1. Chapter 1: Exploring Data
  2. Chapter 2: The normal Distribution
  3. Chapter 3: Examining Relationship
  4. Chapter 4: More on Two-Variable Data

Out of all these four chapter, my most favorite is the examining relationship between the explanatory variable (independent variable) and the response variable (dependent variable) to determine the correlation, form, strength, and the observation association. But the most exciting part of that chapter is finding the least square regression line, which is the line that predicted a response variable at a given response variable. This course will be one of the course that I will put a lot of effort in order to succeed in the AP test, but especially understand the idea behind those data.